Thuật Toán Binary Search
Chào mừng các bạn đến với chủ đề: Thuật toán lập trình.
Bài hôm nay chúng ta cùng tìm hiểu về thuật toán Binary Search, (Thuật toán tìm kiếm nhị phân)
1. Nguyên lý cơ bản của Binary Search.
Giả thuật này hoạt động chính xác khi mà:
danh sách cần tìm kiếm của các bạn đã được sắp xếp theo một thứ tự sẵn có
ví dụ như tăng dần => Đó là lưu ý quan trọng.
Từ yêu cầu như ở trên thì Binary Search sẽ dùng nguyên lý chia để chỉ, nghĩa là phân vùng để tìm kiếm.
Giả định ta có muỗi tập sẵn có xắp xếp theo thứ tự tăng dần.
Tôi giả sử chúng ta có tập dữ liệu từ phần tử a đến phần tử b.
+ Bước 1 sẽ tìm ra phần tử chính giữa hai khoảng a và b.
+ Bước 2 sẽ so sánh phần tử đó với phần tử cần tìm kiếm.
–> Nếu phần tử giữa lớn hơn giá trị cần tìm => các phần tử sau cũng sẽ lớn hơn => lấy khoảng trước.
–> Ngược lại thì ta lấy khoảng sau.
Như vậy một trong hai trường hợp sẽ cho chúng ta một khoảng mới, là khoảng con của tập ban đầu.
Với khoảng mới lại ta lại thực hiện tương tự như ở trên cho đến khi khoảng lấy được càng lúc càng nhỏ dần
cho đến hết số phần tử.
===> Có dấu hiệu của bài toán đệ quy => kỹ thuật áp dụng sẽ là đệ quy.
Minh họa bằng hình vẽ như sau:

CASE 1: Tìm một giá trị có trong tập hợp: Ví dụ 16
+ Vòng 1:
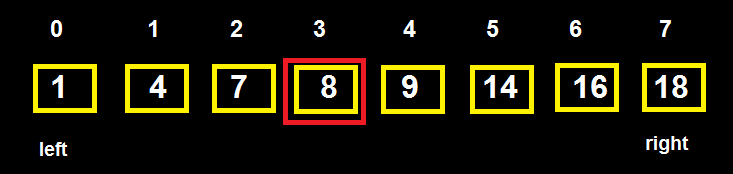
left = 0, right = 7 => mid = left + (right – left)/2 = 3 => T[3] = 8 < 16 => Vòng 2.
+ Vòng 2:
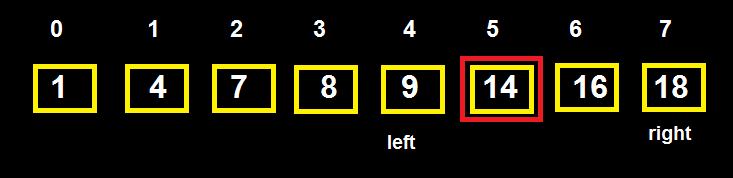
left = mid + 1 = 4, right = 7 => mid = left + (right – left)/2 = 4 + (7 – 4)/2 = 5 => T[5] = 14 < 16 => Vòng 3.
+ Vòng 3:
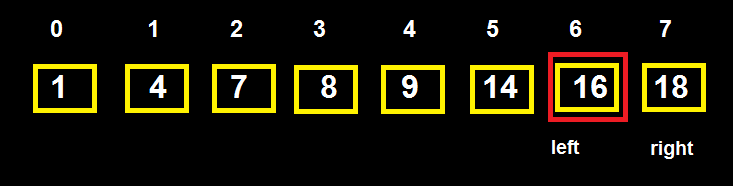
left = mid + 1 = 6, right = 7 => mid = left+ (right – left)/2 = 6 + (7-6)/2 = 6 => T[6] = 16 => Hợp lệ
=> Kết thúc tìm kiếm và show ra kết quả.
CASE 2: Một giá trị không năm trong tập, ví dụ là 100.
Từ vòng 3 ở trên ta có : T[6] = 16 < 100 => Vòng 4
+ Vòng 4:
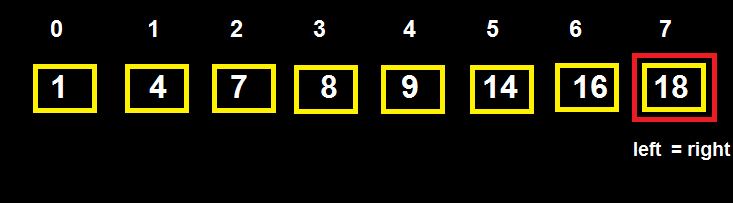
left = mid + 1 = 7, right = 7 => mid = 7 + (7-7)/2 = 7 => T[7] = 18 < 100 => vòng 5.
+ Vòng 5:
left= mid + 1 = 8, right = 7 => Không hợp lệ vì left > right => KẾT THÚC TÌM KIẾM.
OK. Đó là nguyên lý của giải thuật Binary Search, và các bạn có thể tự phân tích cho những giá trị nằm trong các khoảng dưới hoặc giá trị khác.
2. Các tính chất thuật toán Binary Search
– Tập cần tìm kiếm là phải được xắp xếp trước và biết rõ theo chiều tăng giảm.
– Độ phức tạp:
Mỗi vòng thì số phần tử giảm đi còn 1 nửa (tính xấp xỉ).
Lần 1 : số phần tử còn lại là: n/2 = n/2^1.
Lần 2: Số phần tử còn lại là: n/4 = n/2^2.
Lần 3: n/8 = n/2^3.
Như vậy khi kết thúc ta có k lần lặp, và số phần tử còn lại chỉ là 1 phần tử.
=> 1 = n/2^k => n = 2^k => k = Log2(n)
ĐỘ PHỨC TẠP HAY THỜI GIAN THỰC THI CỦA THUẬT TOÁN LÀ: O = Log2(n)
3 Thực hành Thuật Toán Binary Search
Bây giờ từ nguyên lý ở trên chúng ta sẽ cùng thực hành với code c++
// Phattrienphanmem123az.com
#include <iostream>
#include <conio.h>
int BinarySearch(int arr[], const int& left, const int& right, const int& x)
{
if (right >= left)
{
int mid = left + (right - left)/2;
if (arr[mid] == x)
{
return mid;
}
if (arr[mid] < x)
{
int leftp = mid + 1;
return BinarySearch(arr, leftp, right, x);
}
else
{
int rightp = mid - 1;
return BinarySearch(arr, left, rightp, x);
}
}
return -1;
}
Trong hàm main ta xây dựng một tập, và tìm kiếm 1 giá trị.
// Phattrienphanmem123az.com
int main(int argc, _TCHAR* argv[])
{
int arr[] = {1, 4, 7, 8, 9, 14, 16, 18};
int s_val = 8;
unsigned int num = sizeof(arr)/sizeof(arr[0]);
int ret1 = BinarySearch(arr, 0, num -1, s_val);
if (ret1 != -1)
std::cout << "Vi tri cua 16 la: " << ret1;
else
std::cout << "Khong tim dc";
_getch();
return 0;
}
CASE 1: Giá trị tìm kiếm là 8 => kết quả tìm kiếm là 3
CASE 2: Giá trị tìm kiếm là 100 => Không tim thấy.
OK. Đó là nguyên lý và code cơ bản cho thuật toán BinarySearch.
Khi áp dụng vào bài toán thực tế thì, không cơ bản chỉ là giá trị số nguyên thủy mà sẽ là các đối tượng.
Tôi ví dụ một bài toán như sau.
Tôi có một tập hợp các đối tượng.
Đối tượng của tôi là thông tin địa lý và khoảng cách các tỉnh thành việt nam.
Như vậy danh sách của tôi sẽ là một tập hợp các tỉnh thành việt nam được xắp xếp sẵn theo chiều tằng khoảng cách địa lý so với thủ đô Hà Nội.
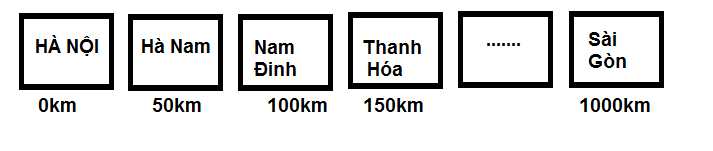
Bài toán yêu cầu:
Tìm xem Thanh Hóa là tỉnh thành thứ bao nhiêu so với hà nội, và nó cách hà nội bao nhiêu km, Cách Đà Nẵng bao nhiêu km.
OK các bạn hay thử nghiên cứu và demo code xem.
TPham

