Thuật Toán Jump Search

Bài hôm nay chúng ta cùng tìm hiểu về thuật toán Jump Search (Thuật toán tìm kiếm nhảy)

1. Nguyên lý cơ bản của Jump Search

Cũng giống như giải thuật Binary Search. Jump Search cũng yêu cầu danh sách đã cho phải là một danh sách đã được sắp xếp theo thứ tự đã biết.

Ví dụ là tăng dần.

Cơ chế của Jump Search đó là tìm ra một hệ số nhảy được tính bằng : Căn bậc hai của số phần tử.

Từ hệ số tìm được, Jump Search sẽ thực hiện nhảy phần tử theo hệ số để tìm ra phần từ lớn hơn giá trị tìm kiếm.

=> Phần tử tìm kiếm sẽ nằm trong khoảng của nhảy mà chứa phần từ lớn hơn giá trị tìm kiếm ở trên.

Minh Họa hình vẽ như sau:

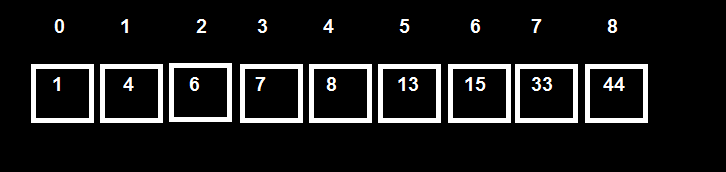
Tôi có tập 9 phần từ đã được sắp xếp theo thứ tự tăng dần.

Tôi xác định giá trị nhảy là step = √9 = 3 .

Giả sử giá trị cần tìm là 33.

Sử dụng một biến prev để lưu vị trí bắt đầu.

Một biến jump để nhảy.

Step 1:

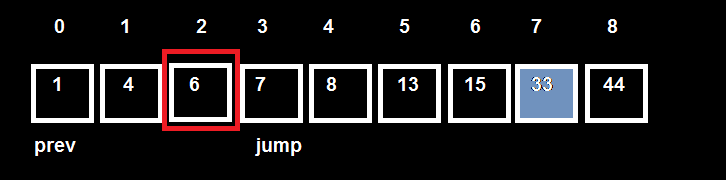
Prev = 0, jump =step = 3

Kiểm tra T[jump – 1] => T[2] = 6 < 33 =>Nhảy step 2.

Step 2:

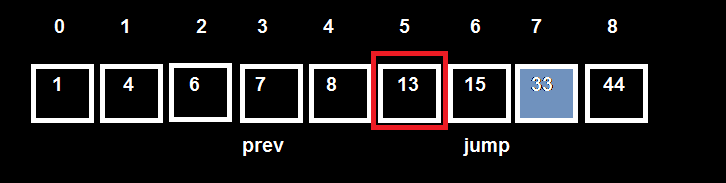
Gán prev = jump = 3.

Nhảy jum theo step => jum = jump + step = 6

Tiếp tục kiểm tra T[jum -1] => T[5] = 13 < 33 => Nhảy step 3

Step 3:

Gán prev = jump = 6

Nhảy jump = jump + step = 9  (bằng số phần tử, nếu jum lớn hơn n thì gán jum = n)

Lại kiểm tra T[jump – 1] => T[8] = 44 > 33 => Đã tìm được khoảng chứa giá trị cần tìm.

Khoảng chứa giá trị cần tìm là từ prev = 6 , jump = 9.

Lúc này chúng ta chỉ việc kiểm tra tuyến tính tệp từ vị trí prev đến jump để tìm ra giá trị cần tìm.

Sử dụng for hoặc while để duyệt phần tử trong khoảng prev – jump.

2. Các tính chất thuật toán.

– Tập cần tìm kiếm là phải được xắp xếp trước và biết rõ theo chiều tăng giảm.

– ĐỘ PHỨC TẠP HAY THỜI GIAN THỰC THI CỦA THUẬT TOÁN LÀ: O = √(n) 

3 Thực hành Jump Search

Bây giờ từ nguyên lý ở trên chúng ta sẽ cùng thực hành với code c++

Hàm JumpSearch

// Phattrienphanmem123az.com
#include <iostream>
#include <conio.h>
#include <math.h>

int JumpSearch(int arr[], const int& n, const int& x)
{
  int step = sqrt(1.0*n);
  int prev = 0;

  int jump = step;
  //Find element > x
  while(arr[jump - 1] < x)
  {
    prev = jump;
    jump +=  step;
    if (jump > n)
      jump = n;
    if (prev > n)
      return -1;
  }

  // When found element > x.
  while(arr[prev] < x)
  {
    prev ++;
    if (prev == jump)
    {
      return -1;
    }
  }

  if (arr[prev] == x)
    return prev;
  return -1;
}

Hàm Main

int main(int argc, _TCHAR* argv[])
{
  int arr[] = {0, 1, 4, 7, 8, 9, 14, 16, 18, 19, 30, 34, 46, 48, 50, 55, 58};
  int s_val = 55;
  unsigned int num = sizeof(arr)/sizeof(arr[0]);
  int ret1 = JumpSearch(arr, num, s_val);

  if (ret1 != -1)
    std::cout << "Vi tri cua " << s_val <<  "la : " << ret1;
  else 
    std::cout << "Khong tim dc";

  _getch();
  return 0;
}

Ok. Đó là nguyên lý cơ bản của JumpSearch.

Về cơ bản thì độ phức tạp thời gian của Jump Search nằm giữa Linear Search (cách tìm kiếm duyệt phần từ thông thường)   và Binary Search.

TPham